数据结构 Tree 各种类别

二叉树的优点

集合有两个常用的实现类

ArrayList LinkedList

这两个集合各自有什么优缺点呢？

ArrayList 可以很方便的全文检索，而 LinkedList 可以很方便的增删元素。但是彼此的优点也是对方的缺点，那有没有一个集大成的数据结构呢？那就是 Tree

Tree 能提高数据存储，读取的效率，比如利用二叉排序树（Binary Sort Tree），既可以保证数据的检索速度，同时也可以保证数据的插入，删除，修改的速度

完全二叉树 Complete Binary Tree

若设二叉树的深度为h，除第 h 层外，其它各层（1～h-1）的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

满足下列性质：

1、只允许最后一层有空缺结点且空缺在右边，即叶子节点只能在层次最大的两层上出现； 2、对任一节点，如果其右子树的深度为 j，则其左子树的深度必为 j 或 j+1。即度为 1 的点只有 1 个或 0 个； 3、除最后一层，第 i 层的节点数是：2i−1； 4、有 n 个节点的完全二叉树，其深度为: $log2n+1$ 或为 $log2n+1$ ； 5、满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

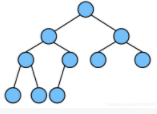
注意：最下面一层一定是从左往右逐步变满的

所以下面这种不是完全二叉树

基于上面那个性质，完全二叉树可以使用数组来表示：

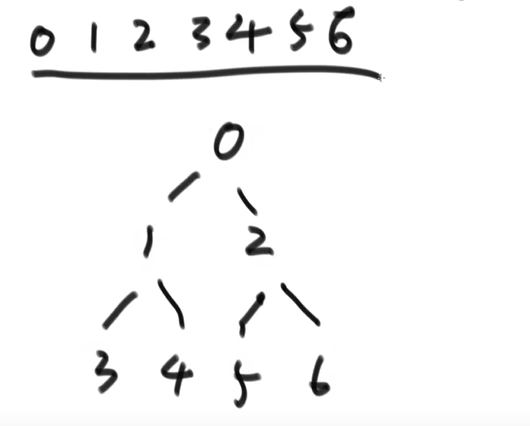
基于此可以直接计算下标的位置：

左：2 * i + 1
右：2 * i + 2
父：(i - 1) / 2

打印数组完全二叉树的工具

这里提供一个打印数组完全二叉树的工具类

代码参考：gist 地址

[93, 97, 92, 87, 49, 54, 60, 84, 40, 7]

生成效果：

              93                              
            92              
    49      54      60      
40  7  

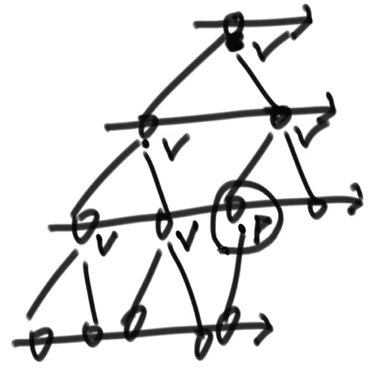
判断是否为完全二叉树

思路： 1、遇到有右孩子，而没有左孩子，则直接返回 false 2、在条件一不违规的条件下，如果遇到了第一个左右子节点不全的情况，后续的节点皆为叶子节点

/**
 * 判读是否为完全二叉树
 */
public static boolean isCBT(TreeNode head) {
    if (head == null) return true;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(head);
    boolean leaf = false; // 满足第一个左右子节点不全的情况时的 flag
    while (!queue.isEmpty()) {
        int length = queue.size();
        for (int i = 0; i < length; i++) {
            TreeNode cur = queue.poll();
            if (cur == null) break;
            if (leaf) {
                if (cur.left != null && cur.right != null) return false;
            }
            // 条件 1
            if (cur.right != null && cur.left == null) return false;
            // 条件 2
            if (cur.left != null && cur.right == null) leaf = true;
            // 相安无事，进行下一轮循环
            if (cur.left != null) queue.add(cur.left);
            if (cur.right != null) queue.add(cur.right);
        }
    }
    return true;
}

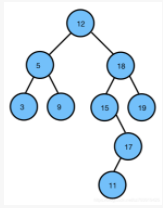
二叉搜索树 Binary Search Tree

又称二叉查找树、二叉排序树（Binary Sort Tree）。

它是一颗空树或是满足下列性质的二叉树：

1、若左子树不空，则左子树上所有节点的值均小于或等于它的根节点的值； 2、若右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值； 3、左、右子树也分别为二叉排序树。

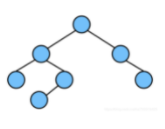
平衡二叉树 Balanced Binary Tree

又被称为 AVL 树，它是一颗空树或左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。

是否为平衡二叉树（DP 法）

平衡条件：

左子树得是平衡的
右子树也得是平衡的
左高 - 右高 <= 1

这里使用上面搜索二叉树的那个套路，分析得需要如下条件

所以判断需要两个条件：是否是平的、高度

/**
 * 判断是否为平衡二叉树
 */
public static boolean isBalancedTree(TreeNode head) {
    return process(head).isBalanced;
}

public static class ReturnType {
    public boolean isBalanced;
    public int height;

    ReturnType(boolean isBalanced, int height) {
        this.isBalanced = isBalanced;
        this.height = height;
    }
}

public static ReturnType process(TreeNode x) {
    if (x == null) return new ReturnType(true, 0);
    // 同样拆黑盒，不用管，总之它代表左边或右边的结果
    ReturnType leftData = process(x.left);
    ReturnType rightData = process(x.right);

    int heightMax = Math.max(leftData.height, rightData.height) + 1;

    boolean isBalanced = leftData.isBalanced && rightData.isBalanced
            && Math.abs(leftData.height - rightData.height) < 2;

    return new ReturnType(isBalanced, heightMax);
}

满二叉树 Full Binary Tree

除最后一层无任何子节点外，每一层上的所有节点都有两个子节点，最后一层都是叶子节点。

满足下列性质：

1、一颗树深度为h，最大层数为k，深度与最大层数相同，k=h； 2、叶子节点数（最后一层）为2k−1； 3、第 i 层的节点数是：2i−1； 4、总节点数是：2k−1，且总节点数一定是奇数。

是否为满二叉树（迭代法）

就是记录节点的个数和层数，最后看是否满足

$N = 2^l - 1$

l = level

/**
 * 判断是否为满二叉树
 */
public static boolean isFBT(TreeNode head) {
    if (head == null) return true;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.add(head);
    int count = 1;
    int level = 0;
    while (!queue.isEmpty()) {
        int length = queue.size();
        for (int i = 0; i < length; i++) {
            TreeNode cur = queue.poll();
            if (cur == null) break;
            if (cur.left != null) {
                count++;
                queue.add(cur.left);
            }
            if (cur.right != null) {
                count++;
                queue.add(cur.right);
            }
        }
        level++;
    }
    return count == (Math.pow(2, level) - 1);
}

是否为满二叉树（DP 法）

按照上面搜索二叉树的方法，总结：判断满二叉树只需两个个条件

高度
节点数量

依旧是之前的套路

    /**
     * 判断是否为满二叉树
     */
    public static boolean isFBT(TreeNode head) {
        ReturnData data = process(head);
        System.out.println(data.height + "   " + data.nodeCount);
        return data.nodeCount == (Math.pow(2, data.height) - 1);
    }

    public static class ReturnData {
        int height;
        int nodeCount;

        public ReturnData(int height, int nodeCount) {
            this.height = height;
            this.nodeCount = nodeCount;
        }
    }

    public static ReturnData process(TreeNode x) {
        if (x == null) return new ReturnData(0, 0);
        // 这里其实就是拆黑盒的过程，不用管它怎么拿到的
        ReturnData leftData = process(x.left);
        ReturnData rightData = process(x.right);

        int height = Math.max(leftData.height, rightData.height) + 1;
        int nodeCount = leftData.nodeCount + rightData.nodeCount + 1;

        return new ReturnData(height, nodeCount);
    }

补充：其实这里的 Math.pow(2, data.height) 可以使用位操作来代替（因为底数是 2）

// 最后一行改成如下：
data.nodeCount == ((1 << data.height) - 1);

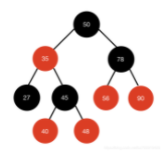
红黑树 Red Black Tree

是每个节点都带有颜色属性（颜色为红色或黑色）的自平衡二叉查找树，就是对上面 AVL 树的改进

满足下列性质：

1、节点是红色或黑色； 2、根节点是黑色； 3、所有叶子节点都是黑色； 4、每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点） 5、从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

霍夫曼树 Huffman Coding

哈夫曼树是一种带权路径长度最短的二叉树，也称为最优二叉树。

给定 n 个权值作为n个叶子结点，构造一棵二叉树，若带权路径长度达到最小，称这样的二叉树为最优二叉树，也称为霍夫曼树(Huffman Tree)

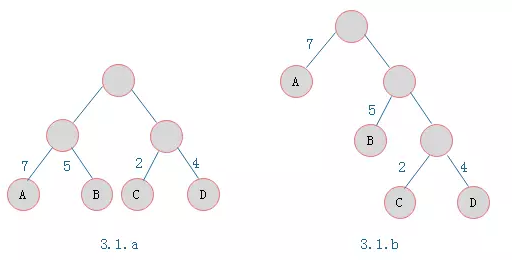
叶子结点为A、B、C、D，对应权值分别为7、5、2、4

3.1.a树的WPL = 7 2 + 5 2 + 2 2 + 4 2 = 36 3.1.b树的WPL = 7 1 + 5 2 + 2 3 + 4 3 = 35

由 ABCD 构成叶子结点的二叉树形态有许多种，但是 WPL 最小的树只有 3.1.b 所示的形态。则 3.1.b 树为一棵霍夫曼树

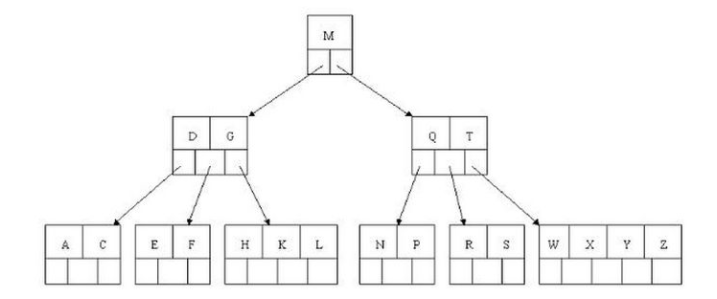
B 树（B- 树）

B 树和平衡二叉树稍有不同的是 B 树属于多叉树又名平衡多路查找树（查找路径不只两个），数据库索引技术里大量使用者 B 树和 B+ 树的数据结构

它是一种树状数据结构，能够用来存储排序后的数据。这种数据结构能够让查找数据、循序存取、插入数据及删除的动作，都在对数时间内完成。

B 树，概括来说是一个一般化的二叉查找树，可以拥有多于2个子节点。与自平衡二叉查找树不同，B 树为系统最优化大块数据的读和写操作。B 树算法减少定位记录时所经历的中间过程，从而加快存取速度。

在 B 树中查找给定关键字的方法是，首先把根结点取来，在根结点所包含的关键字 $K_1,...,K_n$ 查找给定的关键字（可用顺序查找或二分查找法），若找到等于给定值的关键字，则查找成功；否则，一定可以确定要查找的关键字在 $K_i$ 与 $K_i+1$ 之间, $P_i$ 为指向子树根节点的指针，此时取指针 $P_i$ 所指的结点继续查找，直至找到，或指针 $P_i$ 为空时查找失败。

B 树也是一种用于查找的平衡树，但是它不是二叉树。B 树作为一种多路搜索树，它或者是空树，或者是满足下列性质的树：

1、排序方式：所有节点关键字是按递增次序排列，并遵循左小右大原则； 2、子节点数：非叶节点的子节点数 >1，且 <=M ，且 M>=2，空树除外（注：M 阶代表一个树节点最多有多少个查找路径，M = M 路，当 M = 2 则是 2 叉树，M = 3 则是 3叉）； 3、关键字数：枝节点的关键字数量大于等于 $ceil(m/2)-1$ 个且小于等于 M-1 个（注: $ceil()$ 是个朝正无穷方向取整的函数如 $ceil(1.1)$ 结果为 2）; 4、所有叶子节点均在同一层、叶子节点除了包含了关键字和关键字记录的指针外也有指向其子节点的指针只不过其指针地址都为 null 对应下图最后一层节点的空格子;

注：C > B > A

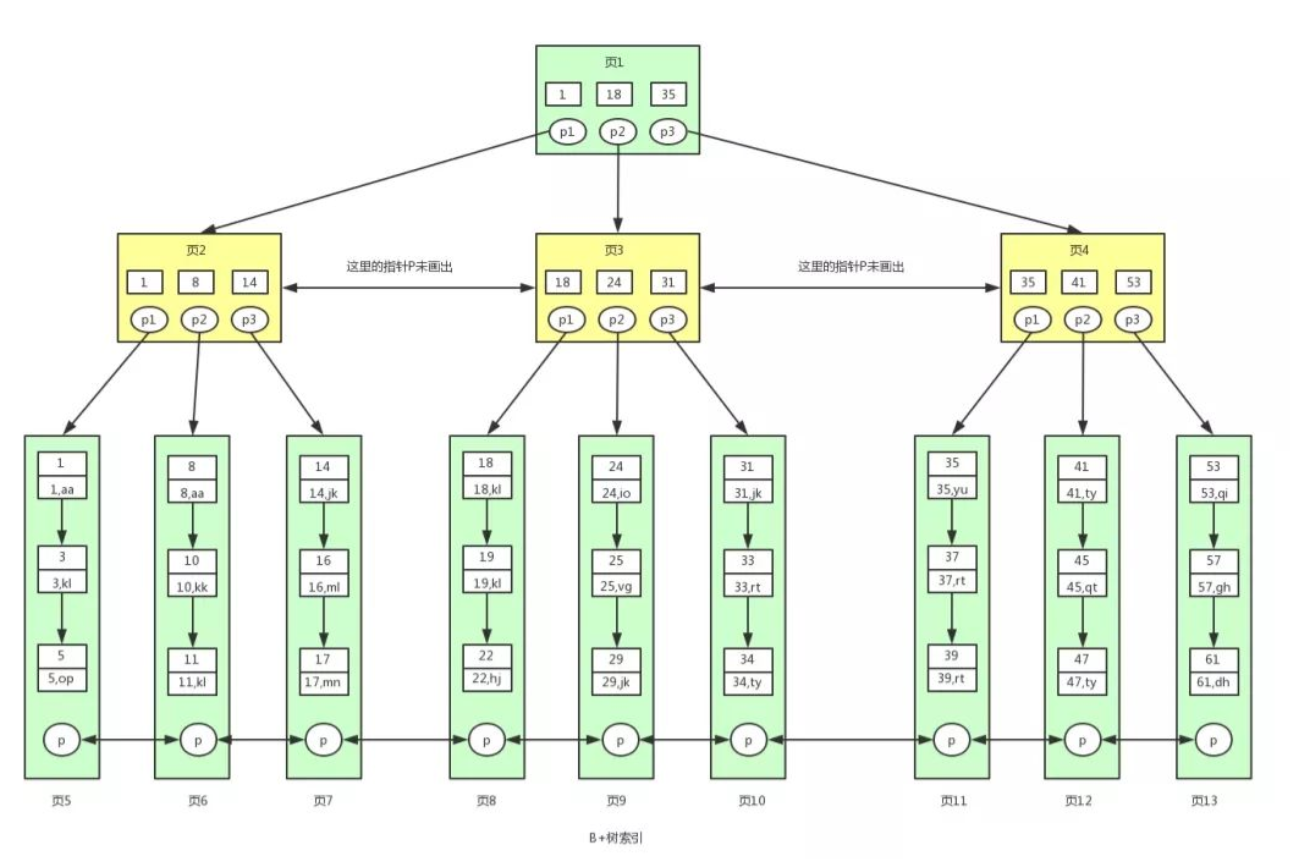
B+ 树

B+ 树是 B树的一个升级版，相对于 B树来说 B+树更充分的利用了节点的空间，让查询速度更加稳定，其速度完全接近于二分法查找。为什么说 B+树查找的效率要比 B树更高、更稳定；我们先看看两者的区别

规则：

1、B+ 跟 B 树不同 B+ 树的非叶子节点不保存关键字记录的指针，只进行数据索引，这样使得 B+ 树每个非叶子节点所能保存的关键字大大增加； 2、B+ 树叶子节点保存了父节点的所有关键字记录的指针，所有数据地址必须要到叶子节点才能获取到。所以每次数据查询的次数都一样； 3、B+ 树叶子节点的关键字从小到大有序排列，左边结尾数据都会保存右边节点开始数据的指针。 4、非叶子节点的子节点数 = 关键字数

哈希树（hash tree 或 Merkle tree）

TODO: 用到再更新...

Trie 树（字典树，前缀树）

TODO: 用到再更新...

Tire 树称为字典树，又称单词查找树。

Trie 树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。

它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

Trie 树的性质：

根节点不包含字符，除根节点外每一个节点都只包含一个字符；
从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串；
每个节点的所有子节点包含的字符都不相同。

Tire 树的应用：

串的快速检索：给出 N 个单词组成的熟词表，以及一篇全用小写英文书写的文章，请按最早出现的顺序写出所有不在熟词表中的生词。在这道题中，可以用数组枚举，用哈希，用字典树，先把熟词建一棵树，然后读入文章进行比较，这种方法效率是比较高的。

“串”排序：给定 N 个互不相同的仅由一个单词构成的英文名，将他们按字典序从小到大输出。用字典树进行排序，采用数组的方式创建字典树，这棵树的每个结点的所有儿子很显然地按照其字母大小排序。对这棵树进行先序遍历即可。

最长公共前缀：对所有串建立字典树，对于两个串的最长公共前缀的长度即他们所在的结点的公共祖先个数，于是，问题就转化为求公共祖先的问题。

二叉树的序列化和反序列化 ⭐

参考左神的教程 2:03:00

就是将内存里的一棵树如何变成字符串形式，又如何从字符串形式变成内存里的树，如何判断一颗二叉树是不是另一棵二叉树的子树？

序列化

序列化时，按照先序遍历的方式读取，遇到 null 时，使用 # 表示

    5
   / \
  1    4
 / \   / \
#   # #   6 
         / \
        #   #
先序遍历
5,1,#,#,4,#,6,#,#

    5
   / \
  4    1
 / \   / \
#   6 #   #
   / \
  #   #
先序遍历
5,4,#,6,#,#,1,#,#

序列化代码：

public static String serialByPre(TreeNode head) {
    if (head == null) return "#_";
    String res = head.value + "_";
    res += serialByPre(head.left);
    res += serialByPre(head.right);
    return res;
}

使用测试：

|       |-------30
|-------91
|       |-------45
96
|       |-------2
|-------66
|       |-------12

96_66_12_#_#_2_#_#_91_45_#_#_30_#_#_

反序列化

反序列化时，也是按照这个顺序进行读取，就可以还原回这颗树了

/**
 * 反序列化
 */
public static TreeNode reconByPreString(String preStr) {
    String[] values = preStr.split("_");
    Queue<String> queue = new LinkedList<>();
    Collections.addAll(queue, values);
    return reconPreOrder(queue);
}

public static TreeNode reconPreOrder(Queue<String> queue) {
    String value = queue.poll();
    if ("#".equals(value)) return null;
    TreeNode node = new TreeNode(Integer.parseInt(value));
    // 因为每次都是从头到最左边，然后再回来，继续到最左边，所以直接使用队列
    node.left = reconPreOrder(queue);
    node.right = reconPreOrder(queue);
    return node;
}

Reference

平衡二叉树、B树、B+树、B*树理解其中一种你就都明白了数据结构学习——树的基本分类 HenleyLee 数据结构-树

二叉树的优点​

完全二叉树 Complete Binary Tree​

打印数组完全二叉树的工具​

判断是否为完全二叉树​

二叉搜索树 Binary Search Tree​

平衡二叉树 Balanced Binary Tree​

是否为平衡二叉树（DP 法）​

满二叉树 Full Binary Tree​

是否为满二叉树（迭代法）​

是否为满二叉树（DP 法）​

红黑树 Red Black Tree​

霍夫曼树 Huffman Coding​

B 树（B- 树）​

B+ 树​

哈希树（hash tree 或 Merkle tree）​

Trie 树（字典树，前缀树）​

二叉树的序列化和反序列化 ⭐​

序列化​

反序列化​

Reference​

二叉树的优点

完全二叉树 Complete Binary Tree

打印数组完全二叉树的工具

判断是否为完全二叉树

二叉搜索树 Binary Search Tree

平衡二叉树 Balanced Binary Tree

是否为平衡二叉树（DP 法）

满二叉树 Full Binary Tree

是否为满二叉树（迭代法）

是否为满二叉树（DP 法）

红黑树 Red Black Tree

霍夫曼树 Huffman Coding

B 树（B- 树）

B+ 树

哈希树（hash tree 或 Merkle tree）

Trie 树（字典树，前缀树）

二叉树的序列化和反序列化 ⭐

序列化

反序列化

Reference